In the previous chapter we looked at supervised learning and comparison: techniques that use known metadata to compare groups.
This is called “supervised” learning it sets as the goal the development of an algorithm that will mimic the operations of some existing classification, like metadata about who wrote a book.
This week, the techniques we’ll discuss are what is known as unsupervised learning; for inferring patterns out of data where you don’t necessarily have data.
Clustering and Unsupervised Modeling
The basic form of clustering is to put data into groups.
We’re going to talk about using a very large number of dimensions–the words in a document. But you can do it on a comparatively smaller number of features, as well. The simplest case is clustering on just two dimensions. Let’s go back to our list of cities as an example to see latitude and longitude-based clustering of cities.
How would you group these points together?
K-means clustering
The simplest method is to choose a fixed number of clusters. An especially widely used form of find the best group of 5 (or 10, or whatever) is k-means clustering. K means is an algorithm that starts by defining a random number of centers, and then assigns each point in your dataset to the closest center’s cluster. It then readjusts each center by making it be the average of all the points in its cluster; and then it checks to see which centers are closest. A nice example video is online here.
The important thing to know about this algorithm is that it can give a different results based on the cluster centers you start with! So a good use of k-means will use a lot of different starting configurations, as defined by the nstart parameter in the code below.
Let’s go back to our data to see how k-means handles the cities. If we ask it for six clusters, we get centers in California, New Mexico, Oklahoma, Indiana, and North Carolina. These are relatively coherent, but the South is sort of divided up; it might be worth trying it with a different number of clusters instead.
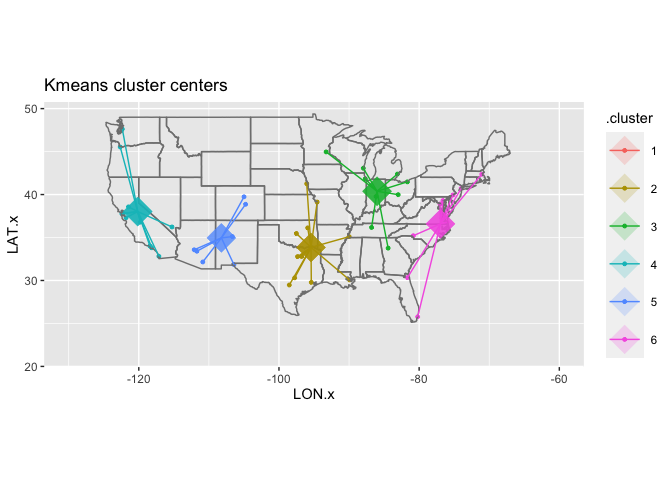
Changing the value of centers gives very different clusterings. There is never a single correct one: you can just choose between a wide variety of them.
Hierarchical Clustering
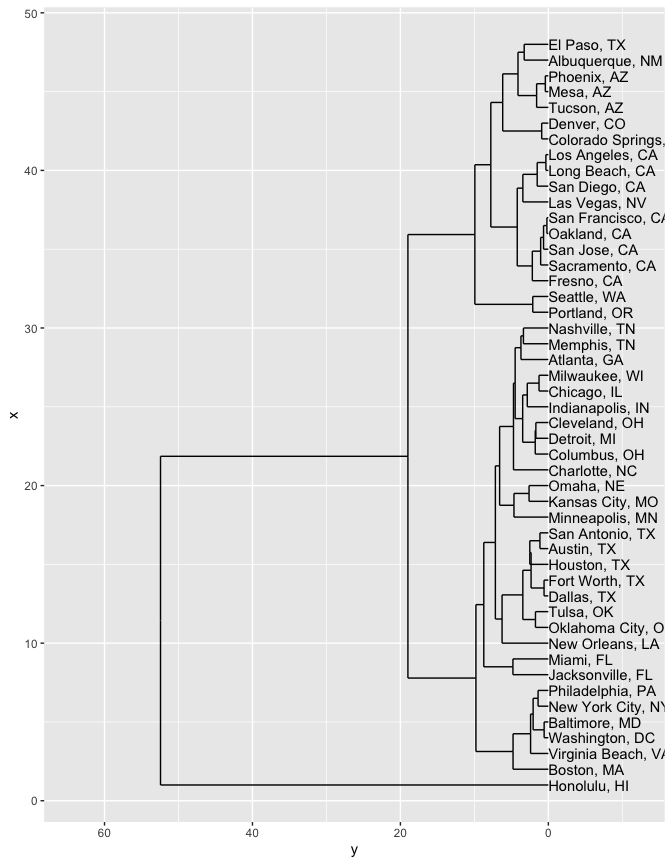
Another method is to build a clustering that works up from the smallest clusters to the largest clusters at once. This tactic is called ‘hierarchical clustering’, and is best visualized using something called a ‘dendrogram’ (or tree-chart; ‘dendro’ is Greek for ‘tree’.)
Hierarchical clustering is a family methods. They find the two closest points, join them together, pretending they’re a single point 1 It then finds the next two closest points, and joins them together; and keeps on going until there’s a single group, encompassing everything.
To train a hierarchical cluster is a two step process. First we create a hierarchical clustering model using the hclust function. Then, to visualize the model, we use the ggdendro package, and two functions inside of it: dendro_data and **segment**.
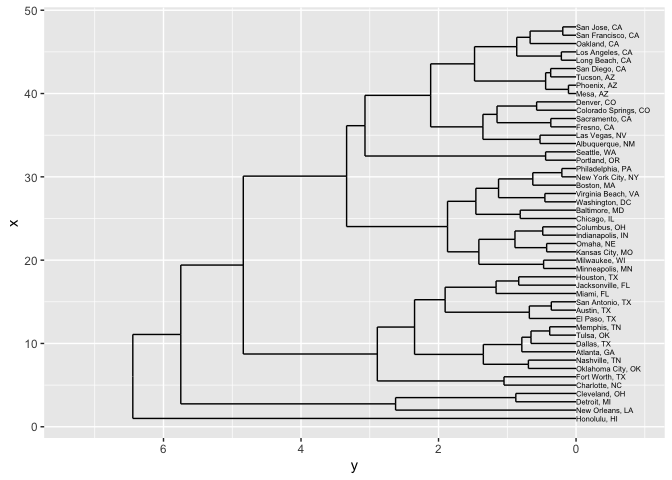
But you could also do a three-dimensional clustering, that relates both location and population change.
The scales will be very different on these, so you can use the R function scale to make them all occupy roughly the same range. (Try fiddling around with some numbers to see what it does, or just put in ?scale.)
That starts to cluster cities together based on things like both location and demographic characteristics. Now the growing cities of San Francisco and San Jose, for instance, are closer to each other than to Oakland: and New Orleans ends up connected to the Rust Belt cities of Detroit and Cleveland because it, too, experienced large population decreases.
A spatialized version of texts is, just as always, a document vectorization. Let’s look again at State of the Unions. A sensible vector space way to cluster them is based on term vectors; here we’ll use a tf_idf version to filter down the impact of extremely common words. (Remember, if you leave in ‘the’ and ‘a’, they will completely dominate any spatial representation of text.)
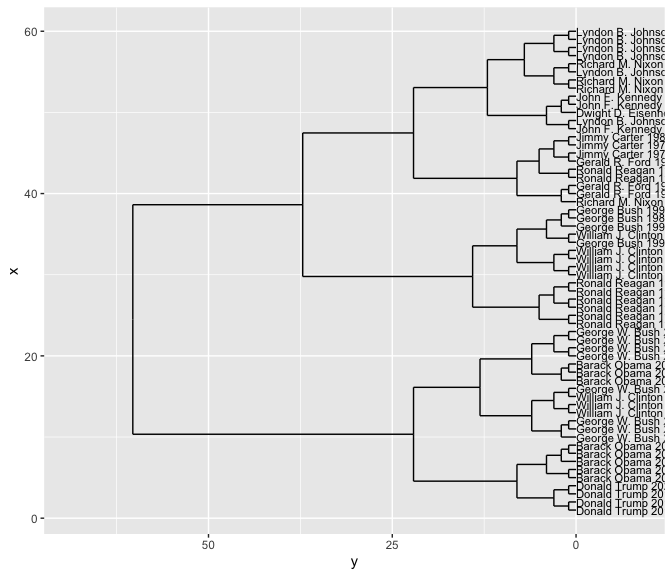
To make a dendrogram, we once again take the distances and plot a hierarchical clustering.
By making the labels be the authors, we can see whether the clusters are grouping similar people together. In this case, it turns out to do quite a good job.
But note that it’s harder in this case to determine whether the same sorts of people are clustered together.
Topic Modeling
“Topic modeling” is the collective name for a class of algorithms that engage in a clever double clustering; every word is distributed across multiple ‘topics,’ and every document is also distributed across the same topics.
Topic modeling is useful as a way of understanding what kinds of words make a corpus up. I consider it a clustering method because it teases out a fixed number of topics without any constraints other than the documents. John Firth’s famous principal of corpus linguistics was that “You shall know a word by the company it keeps.” Topic modeling is one of the best implementations of this strategy, in which words are grouped together just by which documents they appear in.
There are a number of basic introductions to topic modeling that you can access. Within R, there are a number of different applications of topic modeling; in python, the gensim library is widely used. But the best implementation for many purposes is one of the oldest, a program called ‘mallet’ that uses an especially effective algorithm. Mallet is written in the language Java; you can invoke it from inside R, but you will need to install Java as well. The easiest way at present is to install the Adoptium platform.
Mallet is a bit finicky, so it’s worth explaining exactly what we do here.
First, we have to create documents for it to work with: unfortunately, it cannot directly worth from word counts. For our state of the union addresses, we’ll consider a document to be a paragraph. The size of documents is quite important; since a “topic” is “the sort of words that appear in the same document,” shorter working definitions of a “document” will give rise to more tightly defined topics. In general, sensible document lengths are smaller than many humanists suppose–probably closer to a page or paragraph than a full book. To create text, we’ll use summarize to put our individual words back together.
We then need to exclude stopwords, because words like ‘the’, ‘of’, and ‘and’ are so common that they make it impossible to see the real content. Mallet expects stopwords to live in a file, so we write the tidytext list out into a new one.
Then we actually import and build the model. The numbers below are mostly taken from the Mallet documentation; they are a bit more complicated than appear in some other texts (e.g. Silge and Robinson 2019). But the extra steps–especially the “alpha optimization”–make the models significantly better, and you should use these settings for your own models, even if you don’t fully understand them.
Once the model is trained, you can analyze it. Tidytext provides functions that can ‘tidy’ the model into data frames. From these we can create labels. ::: {.cell hash=‘clustering_cache/json/unnamed-chunk-18_379ba6e14556a0e149d7cfbf6daa644d’}
:::
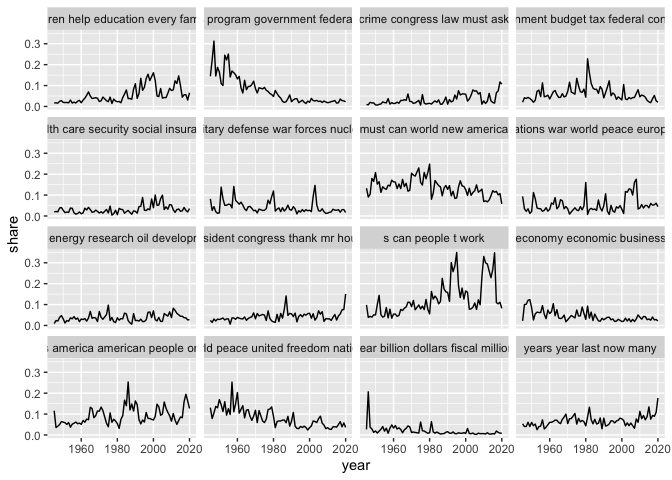
Topics can be interesting to explore on their own, but they can also be used as a measure of similarity in the same way as words but with a much lower number. This process is called dimensionality reduction, and is something we’ll return to later.
This is a simplification–in fact, there are a number of different ways to treat the amalgamated clusters.↩︎