Classifying
Counting data and making comparisons between groups are extremely powerful methods on their own, and the application of more advanced models is not always necessary. But in much recent work in digital humanities, the application of techniques for classifying and clustering have been widely deployed to great effect. And just off their disciplinary shores, in the considerably larger fields of computational social science and computer science, tasks involving prediction, especially, have shaped the horizons of research.
What these features share is that they are fully formed models of the world. Even the most advanced metrics we’ve looked at this far, Dunning’s Log Likelihood, is simply a descriptive statistic; a way of being more precise than an average in describing how several collections differ. The models we need to justify are the data models themselves, but the statistics are transparent in their meaning (if not always easy to understand!). As we enter classification and clustering, we move into something different, where the relations between categories are themselves given weight. In this text I use classifying and clustering essentially synonomously with two more technical terms that you should know: supervised and unsupervised learning. Supervised learning is using some elements in a dataset to predict other elements. You can use word counts to predict the author of a text or its genre; pitch classes to predict the year in which a piece of music was written; the pixels of an image to predict what it shows; or a county’s socioeconomic status to predict the outcome of its votes. Unsupervised learning doesn’t try to predict any particular goal, but instead to make generalizations from within a collection about what elements are like others, or the change the sorts of features in a aset.
Classification
To classify data, let’s start by looking at one of the simplest classification goals: to classify an item into one of two buckets.
As an example work here with the same dataset that Mosteller and Wallace use in their initial authorship attribution study. The file here is an XML document that Matthew Jockers and Daniela Witten created for their 2010 article about authorship attribution; since it is XML, we can use the TEIdy package to read it in and lift the author and title information to each document.
The Federalist papers are a classic text of American government written during the period of debate over the ratification over the constitution. They were written as newspaper articles under pseudonyms (like “Publius”), and a few remained of disputed authorship into the 20th century.
The method we’ll explore here is called logistic regression. It is not the method used by Mosteller and Wallace, who applied far more sophisticated statistical methods than almost anything used in ‘data science’ today. But in general, more data allows you to use less complicated tools; and the the omnipresence of logistic regression means that you’re not so likely to have to explain why you chose it. It represents a widely used swiss-army knife tool to divide items into classes.
#Maybe run: remotes::install_github("HumanitiesDataAnalysis/TEIdy")
fedWords = TEIdytext::TEIdy(
system.file("extdata/federalist.papers.xml", package = "HumanitiesDataAnalysis")) |>
# The 'div' is the basic document level here.
group_by(div) |>
# Any filled-in author fields apply to the whole div.
TEIdytext::lift_data(author) |>
TEIdytext::lift_data(title) |>
# Eliminate things like 'author' and 'title' that occur
# outside of 'text' tags.
filter(text > 0) |>
select(author, title, .text) |>
group_by(author, title) |>
unnest_tokens(word, .text)
Mosteller and Wallace look specifically at function words for classification. So before we go into doing a classification, let’s look at how often each author uses each word, as a share of all words he uses?
function_words = tibble(word = c(
"a", "do", "is", "or", "this", "all", "down",
"it", "our", "to", "also", "even", "its", "shall",
"up", "an", "every", "may", "should", "upon", "and",
"for", "more", "so", "was", "any", "from", "must",
"some", "were", "are", "had", "my", "such", "what",
"as", "has", "no", "than", "when", "at", "have",
"not", "that", "which", "be", "her", "now", "the",
"who", "been", "his", "of", "their", "will", "but",
"if", "on", "then", "with", "by", "in", "one", "there",
"would", "can", "into", "only", "things", "your"
))
authorProbs = fedWords |>
inner_join(function_words) |> # We're using only Mosteller's list.
# For this abstraction, the document is the *author*.
group_by(author, title) |>
count(word) |>
mutate(probability = n / sum(n))
authorProbs |>
filter(author %in% c("HAMILTON", "MADISON")) |>
group_by(author) |>
summarize_llr(word, n)# |>
# arrange(-abs(.dunning_llr))
Naive Bayes
(Incomplete: this is theoretically interesting to think about, but not widely used in practice.)
That new matrix gives us the chance of each author using any individual word. We just need to merge that in, and we can gather the overall probability for any author using the individual words that he or she does. For example, here are the probabilities of each author in our set using the word ‘upon’. If you take a random word, it’s very unlikely that it will be ‘upon’ for any of them; but it’s a lot less unlikely that it’s Hamilton than that it’s Jay or Madison.
Naive Bayesian classifiers by just repeating this over and over again by multiplying possibilities. Multiplying numbers lots of times is hard for computers to track, but this is another case where logarithms are helpful. Maybe you remember from high school math that logarithms let you use addition instead of multiplication. This means that instead of multiplying a string of numbers together, we can simply take the average of their logarithms to see how unlikely the average word is. (We need logarithms for this to be rigorous probability; averaging the percentages is not a good measure.)
Most data science courses talk extensively about linear regression. This is a technique for estimate quantities from other quantities–for instance, you can estimate the amount of money someone has based on their income. While this method is occasionally useful in some digital humanities fields–especially if you touch on economic history–the comparison of two types of quantities is fairly uncommon in digital humanities methods.
Another method, K-nearest-neighbor, predicts classes of items based on a vector space.
A more interpretable method are decision trees. rpart allows training these, but decisions trees are often not especially effective. A method that uses multiple decision trees called random forests is often quite effective, if relatively difficult to interpret. Especially when your data is categorical or difficult to scale, they may be worth exploring. The package randomForest provides random forests.
Logistic Regression
One species of linear regression, called logistic regression has become the overwhelmingly popular way of performing classifications in the digital humanities, perhaps because it does not generally rely on refined statistical assumptions about distributions.
We’ll explore it first through the authorship problem in the Federalist papers. We’ll do this, for the time being, by aiming to predict solely whether the unknown Federalists are by Hamilton or Madison.
First we’ll create a term document matrix as in the last chapter.
fedMatrix = authorProbs |>
select(word, probability, author, title) |>
pivot_wider(names_from = word, values_from = probability, values_fill = c(probability = 0)) |>
ungroup() |>
mutate(title = title |> str_extract("[0-9]+") |> as.numeric())
known = fedMatrix |> filter(author %in% c("HAMILTON", "MADISON"))
unknown = fedMatrix |> filter(author == "DISPUTED")
This gives us a data frame where two columns are the author and the title, and the rest are the shares of various different words.
Then we run the model. In R, logistic regression is contained inside the glm function, which allows you run many different types of models.
This returns a model object, which is quite different than the tidy data we’ve been working with, and more like the PCA models we saw before.
You can inspect the output of a model by calling the ‘summary’ function. The most important statistics here are the coefficients table; here you can read codes that tell you if the model is finding statistically significant patterns. The general standard for significance is a 95% chance that the result isn’t random, represented by a p value under 0.05. Here, the best score we get is 0.06; you could call that ‘weakly significant’, but fortunately this kind of equivocation is getting pushed out of the social sciences and has never become widespread in the humanities.
Note the special syntax of the glm function. The first argument is the phrase is_hamilton ~ there + by + on. is_hamilton is a logical value defined the code, and there + by + on are the wordcounts we will use to predict it. In between is a squiggly line, ~. We’ve already seen it a bit in other functions. In R you can read the squiggly line as meaning “in terms of” or “as a function of.”
known = known |> mutate(is_hamilton = author == "HAMILTON")
model = glm(
is_hamilton ~ there + by + on,
data = known, family = "binomial")
model |> summary()
More relevant is how powerful these features are. We can use the model to create a new row of predictions on the combination.
You may have heard that computers think in binary categories and humans think in subtle shades. With authorship, as with much else, the truth is precisely the opposite: while we can know that a particular paper is by Hamilton, a logistic model will only ever put out a probability.
These predictions are, yet again, a form of log transformation. They are, though, a special type of transformation known as the ‘log odds,’ which can be converted to a probability using the so-called ‘logistic function.’ They are ‘odds’ in the betting sense; the log-odds treat a bet like “3 to 1 odds” as a fraction and take the logarithm of it.
The raw output of a logistic regression are numbers of any size: a ‘0’ indicates that the model predicts an even chance of the label belonging to either class: as the numbers grow larger they asymptotically approach certainty that it belongs to the class used to train the model, and lower and lower negative numbers indicate progressively higher chances that the label does not apply.
You might say, for instance, that something has a “million-to-one odds”” of happening; since the natural log of one million is 13.8, that would be expressed as a chance of -13.8. Odds of 95 to 5–that traditional significance interval–are about -2.94; anything in between -2.94 and 2.94 is an uncertain guess.
The chart below shows the predictions of our logistic model in both of these dimensions: normally you’d likely only look at the log odds, because using probabilities tends to cluster things too tightly.
As you can see, our little model seems to be doing a pretty good job: most of the Hamilton has a high probability of being Hamilton-written, and most of the Madison is on the left.
The disputed papers are generally listed as being more likely by Madison, with one exception that looks kind of like a Hamilton-authored paper.
predictions = fedMatrix |>
mutate(number = title |> str_extract("[0-9]+") |> as.numeric()) |>
modelr::add_predictions(model, var = ".prediction") |>
select(author, number, .prediction)
predictions |>
ggplot() +
geom_point(aes(y = .prediction, x = plogis(.prediction), color = author, pch = author), size = 3) +
labs(title = "Model outputs and certainty by Federalist paper.") + scale_x_continuous(labels = scales::percent)
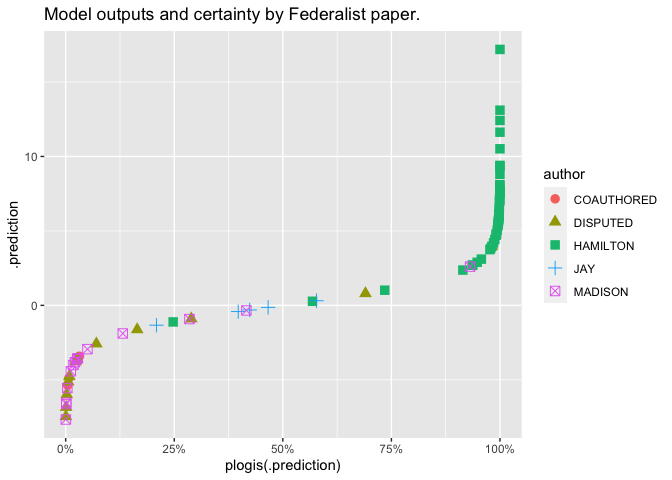
This looks great! But actually, this provides too much certainty, because we’re committing the cardinal sin of data analysis: mixing our test and training data. It’s not right to evaluate the performance of a model on the same data we trained it on; the model can easily be overfitted.
The right way to handle this is to break into test and training sets.
In the tidyverse, we can do this in two steps: first create a test set by sampling 1 in 4 documents randomly, then assigning the rest to a train set using an anti_join function. There are, of course, other ways; but the relational algebra one works well.
set.seed(1)
test = known |> sample_frac(.25)
train = known |> anti_join(test, by = c("title"))
Then we fit a new model using glm again.
model = glm(author == "HAMILTON" ~ there + by + on, data = train, family = "binomial")
predictions = test |>
modelr::add_predictions(model, var = ".prediction") |>
select(author, title, .prediction)
predictions |>
ggplot() +
geom_point(aes(y = .prediction, x = plogis(.prediction), color = author, pch = author), size = 3)
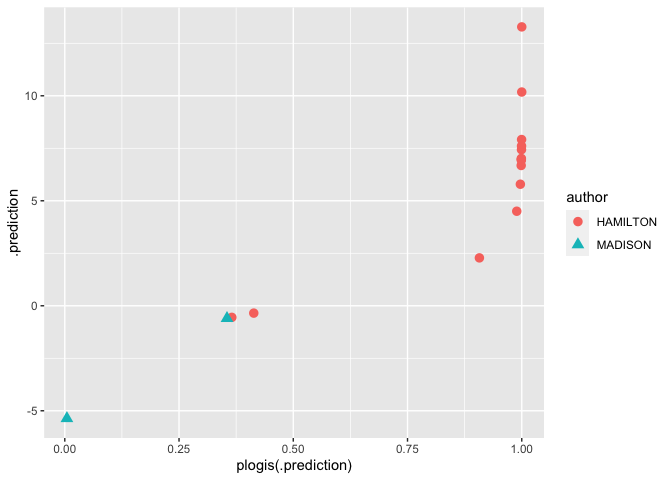
Thinking about errors requires more than just blindly sampling, though.
Consider predicting the party of an American president based on their stopword usage. We’ll run a classification of whether a president is a “Democrat” or not, allowing all the other various parties to blend together.
Again, we drop down to common words; and pivot out the counts to make them into columns
president_mat = get_recent_SOTUs(1860) |>
group_by(word) |>
filter(n() > 7500) |>
group_by(year, president, party) |>
count(word) |>
mutate(share = n / sum(n)) |>
select(-n) |>
pivot_wider(names_from = word, values_from = share, values_fill = c(share = 0)) |>
ungroup()
set.seed(3)
test = president_mat |> sample_frac(.2)
train = president_mat |> anti_join(test, by = "year")
model = glm(party == "Democratic" ~ . + 0, data = train |> select(-president, -year), family = "binomial")
summary(model)
Once again, we can use predict on a model to see what we get. Remember that predicted values over 0 mean ‘TRUE’ and those below 0 mean FALSE. Here we can use the count() function to see how often we get the correct answer right.
test_fit = test |> mutate(predicted = predict(model, newdata = test))
test_fit |>
mutate(prediction = ifelse(predicted > 0, "Democratic", "Republican")) |>
mutate(correct = prediction == party) |>
count(correct) |>
mutate(
rate = n / sum(n)
)
Choose a different collection of texts that you can divide into two classes. Copying the democratic/republican code above, attempt to predict the variable using textual features.
Choose two states, and create a dataframe from the cities datasets we’ve been working with. Create some new columns which show population change between different censuses. (Note–you will have the best results if you make change be the logarithm of the change–e.g., change_from_1950_to_1960 = log(\1960` / `1950)``.)
Use glm with a binomial model to predict what state a city is in based on some of these population shifts. Then inspect the probabilities to see which cities it’s especially wrong on. Can you tell why? (You’ll probably have to look up the cities to tell what’s going on–it’s OK to use drop_na to get rid of entries that prevent things were working on.)
Choosing the right test and train sets
You might be tempted to think that this is a remarkable finding! 85% percent of the time, we can predict whether or not a person is a Republican or Democrat simply from the stopwords that they use.
But there are few problems. First, 85% needs to be considered against a baseline of 50%; even if you guess randomly, you’ll be right half the time. Second, this is a misleading sample. Although we are technically predicting party, we have still allowed our test and training data to become conmingled in a way, because we have multiple examples from each president.
This is another level of address problem. We need to think of what the groups we’re really comparing are. Here, we’re better off splitting the presidents into test and train sets, and then building our sets up from that.
Finally, this is a tricky sample! Why did I choose 1860? Because it got the best results!
set.seed(1)
test_presidents = president_mat |>
distinct(president) |>
sample_frac(.25)
test = president_mat |> inner_join(test_presidents)
train = president_mat |> anti_join(test_presidents)
model = glm(party == "Democratic" ~ ., data = train |> select(-president, -year), family = "binomial")
summary(model)
test_fit = test |> modelr::add_predictions(model, var = "predicted")
test_fit |>
mutate(prediction = ifelse(predicted > 0, "Democratic", "Republican")) |>
mutate(correct = prediction == party) |>
count(correct) |>
mutate(
rate = n / sum(n)
)
test_fit |> mutate(prob = plogis(predicted)) |>
ggplot() + geom_point(aes(x = year, y = prob, color=party))
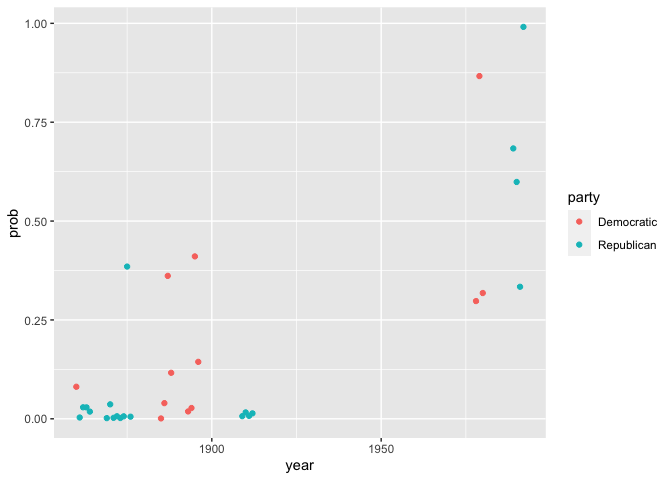
Problems of authorship attribution in the digital humanities have developed a much more robust statistical literature to deal with these kinds of problems, because they frequently have to work with extremely small samples like those here. To learn more about this specialized area of discourse, you’ll want to look into the archives of Digital Scholarship in the Humanities.
But in non-authorship questions, digital humanists have been comparatively more relaxed. Rather than worry too much about the mathematics of statistical distributions, they have looked for problems where the data is large enough that we can use logistic regression with adequate controls.
- Choose a different set of documents and compare them along some metadata facet by PMI, Dunning Log-Likelihood, and (if applicable) TF-IDF. Plot the results in some way, separately or together.
(Hard, skippable.) Build a logistic classifier to predict the class of a book based on its synopsis. You can use “Juvenile literature,” or find another frequent category.
Calculate the classifiers accuracy (the percentage of predictions that are correct). Look at the highest-likelihood misclassifications in both directions to see why it might be getting it wrong.
titles = books |>
mutate(.juvenile = subjects |> str_detect("Juvenile literature"))
# Turn titles into a term document matrix with just the class.
tdMatrix = titles |>
select(.juvenile, lccn, summary) |>
unnest_tokens(word, summary) |>
group_by(word) |>
filter(n() > 5000) |>
group_by(word, lccn, .juvenile) |>
summarize(count = n()) |>
group_by(lccn) |>
pivot_wider(names_from = word, values_from = count, values_fill = c(count = 0)) |>
ungroup
# etc: fill it out from here using spread, filter, etc. Make sure to limit the
# population of words before you run "pivot_wider."
# Split into test and training data using the lccns.
# This will keep you honest. (Is it an unfair split?)
# The particular function here: `%%` tests if the number
# is divisible by nine. This means one in nine books
# will be in the test set.
train = tdMatrix |> filter(lccn %% 9 != 0)
test = tdMatrix |> filter(lccn %% 9 == 0)
model = glm(.juvenile ~ ., data = train |> select(-lccn), family = "binomial")
summary(model)
test |> mutate(prediction = predict(model, newdata = test)) |> arrange(-prediction) |>
head(10) |>
inner_join(books, by = c(".lccn" = "lccn"))
Free Exercise. Re-using your code from 3 as much as possible, train some other classificatory model. It can use textual features or something else.